Assignment 6 2D Transformation
AIM: Implement following 2D transformations on the object with respect to axis :
i) Scaling ii) Rotation about arbitrary point iii) Reflection iv)Translation
Translation: Translation is defined as moving the object from one position to another position along
straight line path.
We can move the objects based on translation distances along x and y axis. tx denotes translation distance along x-axis and ty denotes translation distance along y axis.
Translation Distance: It is nothing but by how much units we should shift the object from one location to another along x, y-axis.
Consider (x,y) are old coordinates of a point. Then the new coordinates of that same point (x’,y’) can be obtained as follows:
X’=x+tx
Y’=y+ty
Scaling: scaling refers to changing the size of the object either by increasing or decreasing. We will increase or decrease the size of the object based on scaling factors along x and y -axis.
If (x, y) are old coordinates of object, then new coordinates of object after applying scaling
transformation are obtained as:
x’=x*sx
y’=y*sy.
sx and sy are scaling factors along x-axis and y-axis. we express the above equations in matrix form as:
Rotation : A rotation repositions all points in an object along a circular path in the plane centered at the
pivot point. We rotate an object by an angle theta
New coordinates after rotation depend on both x and y
x’ = xcosθ -y sinθ
y’ = xsinθ+ ycosθ
or in matrix form:
P' = R • P,
R-rotation matrix.
Formula: X = xcosA - ysinA
Y = xsinA + ycosA,
A is the angle of rotation.
The above formula will rotate the point around the origin.
To rotate around a different point, the formula:
X = cx + (x-cx)*cosA - (y-cy)*sinA,
Y = cx + (x-cx)*sinA + (y-cy)*cosA,
cx, cy is centre coordinates,
A is the angle of rotation.
The OpenGL function is glRotatef (A, x, y, z). 
Reflection: It is a transformation which produces a mirror image of an object. The mirror image can be either about x-axis or y-axis. The object is rotated by180°.
Types of Reflection:
- Reflection about the x-axis
- Reflection about the y-axis
- Reflection about an axis perpendicular to xy plane and passing through the origin
- Reflection about line y=x
1. Reflection about x-axis: The object can be reflected about x-axis with the help of the following matrix
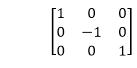
In this transformation value of x will remain same whereas the value of y will become negative. Following figures shows the reflection of the object axis. The object will lie another side of the x-axis.
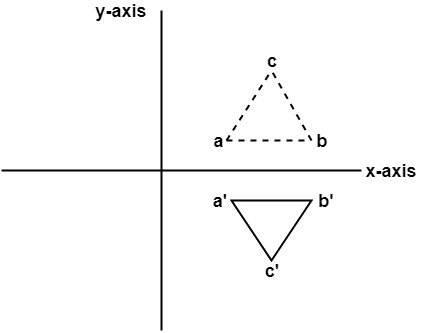
2. Reflection about y-axis: The object can be reflected about y-axis with the help of following transformation matrix
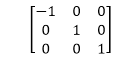
Here the values of x will be reversed, whereas the value of y will remain the same. The object will lie another side of the y-axis.
The following figure shows the reflection about the y-axis
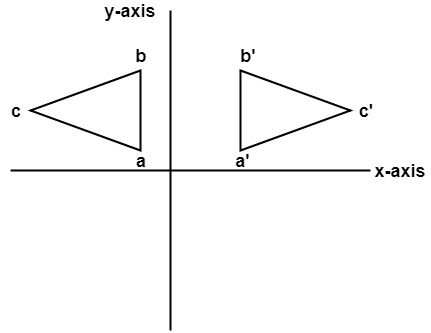
3. Reflection about an axis perpendicular to xy plane and passing through origin:
In the matrix of this transformation is given below
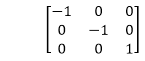
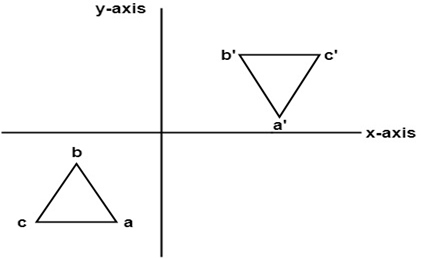
In this value of x and y both will be reversed. This is also called as half revolution about the origin.
4. Reflection about line y=x: The object may be reflected about line y = x with the help of following transformation matrix
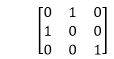
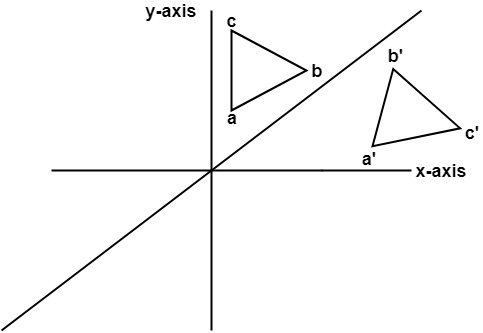
First of all, the object is rotated at 45°. The direction of rotation is clockwise. After it reflection is done concerning x-axis. The last step is the rotation of y=x back to its original position that is counterclockwise at 45°.
Example: A triangle ABC is given. The coordinates of A, B, C are given as
A (3 4)
B (6 4)
C (4 8)
Find reflected position of triangle i.e., to the x-axis.
CODE
#include <iostream>
#include <math.h>
#include <time.h>
#include <GL/glut.h>
#include <vector>
using namespace std;
int edge;
vector<int> xpoint;
vector<int> ypoint;
int ch;
double round(double d){
return floor(d + 0.5);
}
void init(){
glClearColor(1.0,1.0,1.0,0.0);
glMatrixMode(GL_PROJECTION);
gluOrtho2D(0,640,0,480);
glClear(GL_COLOR_BUFFER_BIT);
}
void translation(){
int tx, ty;
cout<<"\t Enter Tx, Ty \n";
cin>> tx>> ty;
//Translate the point
for(int i=0;i<edge;i++){
xpoint[i] = xpoint[i] + tx;
ypoint[i] = ypoint[i] + ty;
}
glBegin(GL_POLYGON);
glColor3f(0,0,1);
for(int i=0;i<edge;i++){
glVertex2i(xpoint[i],ypoint[i]);
}
glEnd();
glFlush();
}
void rotaion(){
int cx, cy;
cout<<"\n Enter Ar point x , y ";
cin >> cx >> cy;
cx = cx+320;
cy = cy+240;
glColor3f(0.0, 1.0, 0.0);
glBegin(GL_POINTS);
glVertex2i(cx,cy);
glEnd();
glFlush();
double the;
cout<<"\n Enter thetha ";
cin>>the;
the = the * 3.14/180;
glColor3f(0,0,1.0);
glBegin(GL_POLYGON);
for(int i=0;i<edge;i++){
glVertex2i(round(((xpoint[i] - cx)*cos(the) - ((ypoint[i]-cy)*sin(the))) + cx),
round(((xpoint[i] - cx)*sin(the) + ((ypoint[i]-cy)*cos(the))) + cy));
}
glEnd();
glFlush();
}
void scale(){
glColor3f(1.0,0,0);
glBegin(GL_POLYGON);
for(int i=0;i<edge;i++){
glVertex2i(xpoint[i]-320,ypoint[i]-240);
}
glEnd();
glFlush();
cout<<"\n\tIn Scaling whole screen is 1st Qudrant \n";
int sx, sy;
cout<<"\t Enter sx, sy \n";
cin>> sx>> sy;
//scale the point
for(int i=0;i<edge;i++){
xpoint[i] = (xpoint[i]-320) * sx;
ypoint[i] = (ypoint[i]-240) * sy;
}
glColor3f(0,0,1.0);
glBegin(GL_POLYGON);
for(int i=0;i<edge;i++){
glVertex2i(xpoint[i],ypoint[i]);
}
glEnd();
glFlush();
}
void reflection(){
char reflection;
cout<<"Enter Reflection Axis \n";
cin>> reflection;
if(reflection == 'x' || reflection == 'X'){
glColor3f(0.0,0.0,1.0);
glBegin(GL_POLYGON);
for(int i=0;i<edge;i++){
glVertex2i(xpoint[i], (ypoint[i] * -1)+480);
}
glEnd();
glFlush();
}
else if(reflection == 'y' || reflection == 'Y'){
glColor3f(0.0,0.0,1.0);
glBegin(GL_POLYGON);
for(int i=0;i<edge;i++){
glVertex2i((xpoint[i] * -1)+640,(ypoint[i]));
}
glEnd();
glFlush();
}
}
void Draw(){
if(ch==2 || ch==3 || ch==4){
glColor3f(1.0,0,0);
glBegin(GL_LINES);
glVertex2i(0,240);
glVertex2i(640,240);
glEnd();
glColor3f(1.0,0,0);
glBegin(GL_LINES);
glVertex2i(320,0);
glVertex2i(320,480);
glEnd();
glFlush();
glColor3f(1.0,0,0);
glBegin(GL_POLYGON);
for(int i=0;i<edge;i++){
glVertex2i(xpoint[i],ypoint[i]);
}
glEnd();
glFlush();
}
if(ch==1){
scale();
}
else if(ch == 2){
rotaion();
}
else if( ch == 3){
reflection();
}
else if (ch == 4){
translation();
}
}
int main(int argc, char** argv){
cout<<"\n \t Enter 1) Scaling ";
cout<<"\n \t Enter 2) Rotation about arbitrary point";
cout<<"\n \t Enter 3) Reflection";
cout<<"\n \t Enter 4) Translation \n \t";
cin>>ch;
if(ch==1 || ch==2 || ch==3 || ch==4){
cout<<"Enter No of edges \n";
cin>> edge;
int xpointnew, ypointnew;
cout<<" Enter"<< edge <<" point of polygon \n";
for(int i=0;i<edge;i++){
cout<<"Enter "<< i << " Point ";
cin>>xpointnew>>ypointnew;
xpoint.push_back(xpointnew+320);
ypoint.push_back(ypointnew+240);
}
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);
glutInitWindowSize(640,480);
glutInitWindowPosition(200,200);
glutCreateWindow("2D");
init();
glutDisplayFunc(Draw);
glutMainLoop();
return 0;
}
else{
cout<<"\n \t Check Input run again";
return 0;
}
}
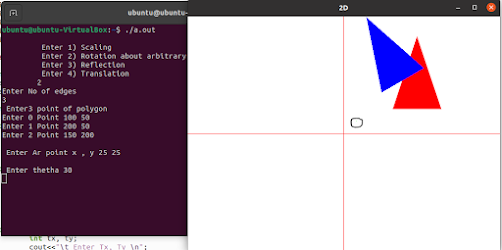
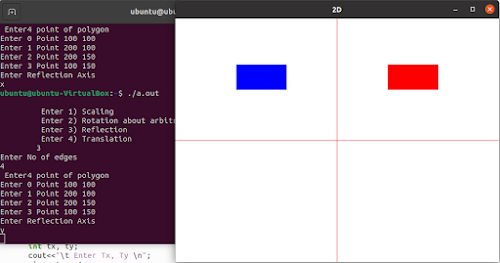
OUTPUT
g++ filename.cpp -lGL -lGLU -lglut
./a.out
FAQWhat is homogeneous co-ordinate system ?



Comments
Post a Comment